How To Find If Two Space Curves Intersect

When a parabola and circle intersect, the possibilities for their meeting are many and varied. The two curves tin intersect in as many equally four different points, or maybe 3, or merely 2 or even simply 1 signal.

Keep your options open and be alert for as many common solutions as possible (right — up to four). And, yes, the organization may have no solution at all. The curves may miss each other completely.

For these issues, you usually turn to substitution. However, you lot don't take to set i of the equations equal to x or y by itself. You lot may solve an equation for fourx or (y – 3)^two or some other term that appears in the other equation. Every bit long every bit the terms match, you can swap ane value for the other.

Sample questions

Find the mutual solutions of the circle (10 – 2)^two + (y – 2)² = four and the parabola 2y = 10 ⁱⁱ – 410 + 4.

(0, two), (2, 0), (4, 2). Rewrite the equation of the parabola as 2y = (10 – 2)². Next, replace the (x– two)² term in the first equation with iiy and simplify: 2y + (y – two)² = 4; 2y + y ² – 4y + four = four; y ² – 2y = 0.

Cistron the terms on the left to become y(y – 2) = 0. Then, y = 0 or y = 2. Letting y = 0 in the equation of the parabola, you become two(0) = ten ² – 4x + four, or 0 = (ten – 2)². And then, when y = 0, 10 = 2.

Side by side, let y = 2 in the parabola equation. You get 2(2) = 10 ⁱⁱ – iv10 + 4; 4 = x ² – 4x + 4; 0 = x ^two – 4ten. Factoring, 0 = 10(x – 4), so x = 0 or ten = 4. When y = 2, x = 0 or 4.
Find the mutual solutions of ten ² + y ² = 100 and y ² + 6x = 100.

(0, 10), (0, –10), (vi, 8), (6, –8). Solving the second equation for y ⁱⁱ, you get y ² = 100 – half dozenx. Replace the y ^two in the first equation with its equivalent to become x ² + 100 – half-dozenx = 100.

Simplifying and factoring, the equation becomes 10 ² – 610 = x(x – vi) = 0. So ten = 0 or x = six. Replacing x with 0 in the equation of the parabola, y ² = 100; y = +/–10. Replacing ten with half dozen in the equation of the parabola, y ² + 36 = 100; y ² = 64; y = +/–viii.

Practice questions

Find the mutual solutions of x ² + y ⁱⁱ = 25 and ten ² + foury = 25.
Find the common solutions of x ² + y ² = 9 and 510 ² – sixy = xviii.

Following are answers to the practice questions:

The answer is (5, 0), (–5, 0), (3, four), (–three, iv).

Solve the 2d equation for x ² (you lot get x ² = 25 – foury) and supercede the ten ² in the first equation with its equivalent. The new equation reads 25 – 4y + y ² = 25. Simplifying, you get y ² – 4y = 0.

This equation factors into y(y – 4) = 0. The two solutions are y = 0 and y = four. Go back to the second equation, the equation of the parabola, because it has only 1 squared term (it has lower exponents, so choosing this equation lets you avert extraneous solutions).

Supervene upon the y in that equation with 0 to get x ² + 4(0) = 25; x ² = 25. That equation has two solutions: x = v or x = –5. Now, going back and replacing the y with 4 in the equation of the parabola, x ² + 4(iv) = 25; x ⁱⁱ + xvi = 25; 10 ⁱⁱ = ix.

This equation as well has two solutions: 10 = 3 or ten = –three. Pairing up the y'southward and their respective ten's, you get the four different solutions. The circumvolve and parabola intersect in four distinct points.
The respond is

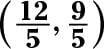
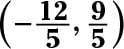
(0, –3).

Eliminate the x terms: Multiply the terms of the first equation by –5 (which gives y'all –vx ² – vy ²= –45) and add the two equations together. The resulting equation is –vy ² – 6y = –27.

Rewrite the equation, setting it equal to 0, and factor. Yous become 0 = 5y ² + 6y – 27 = (fivey – 9)(y + 3). Use the multiplication holding of zero to solve for the ii solutions of this equation. Replacing the y in the 2d equation (the equation of the parabola) with

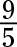
you become

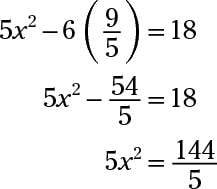
Then divide both sides of the equation by 5 and have the foursquare root of each side:

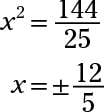
To find the other solution, let the y in the equation of the parabola exist equal to –3. You lot go 5ten ² – 6(–iii) = 18; 5x ^two + 18 = xviii; 5x ² = 0. So, 10 = 0. The circle and parabola intersect or touch in three distinct points.